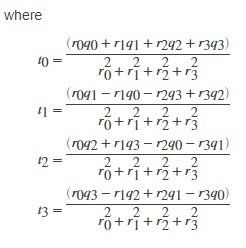Unreal Engine Study

mainwindow.h

#ifndef MAINWINDOW_H
#define MAINWINDOW_H

#include  <QMainWindow>
#include  <QTimerEvent>
#include  <QPaintEvent>

class MainWindow : public QMainWindow
{
    Q_OBJECT
    QPolygon *polygon;
    QPointF pts[4];

public:
    MainWindow(QWidget *parent = 0);
    ~MainWindow();

    void paintEvent(QPaintEvent* e);
    void timerEvent(QTimerEvent *e);
    void rotateRect(float a);
};

#endif // MAINWINDOW_H

mainwindow.cpp

#include "mainwindow.h"
#include  <QPainter>
#include  <QPolygon>
#include  <cmath>

MainWindow::MainWindow(QWidget *parent)
    : QMainWindow(parent)
{
    //원점을 중심으로 위치한 정사각형의 꼭지점 좌표
    pts[0] = QPointF(-50,-50);
    pts[1] = QPointF(50,-50);
    pts[2] = QPointF(50,50);
    pts[3] = QPointF(-50,50);

    polygon = new QPolygon(4); // 4개의 꼭지점을 갖는 다각형
    for(int i=0;i<4;i++){
        polygon->setPoint(i,pts[i].x(),pts[i].y());
    }

    startTimer(50);
}

MainWindow::~MainWindow(){}

void MainWindow::paintEvent(QPaintEvent *e)
{
    QPainter painter(this);
    rotateRect(0.1F);
    painter.setBrush(QBrush("#ff0000"));
    painter.drawPolygon(*polygon);
}

void MainWindow::timerEvent(QTimerEvent *e)
{
    repaint();
}

void MainWindow::rotateRect(float a)
{
    /* 행렬을 이용한 점(벡터)의 회전(원점을 중심으로 Θ라디안 회전)
     cos(Θ), -sin(Θ)        px
     sin(Θ), cos(Θ)     *   py
     -------------------------
     x' = cos(Θ)*px - sin(Θ)*py
     y' = sin(Θ)*px + cos(Θ)*py
    */

    for(int i=0;i<4;i++){
        float x = cos(a)*pts[i].x() - sin(a)*pts[i].y();
        float y = sin(a)*pts[i].x() + cos(a)*pts[i].y();
        pts[i].setX(x);
        pts[i].setY(y);
        polygon->setPoint(i,
           pts[i].x()+width()/2,
           pts[i].y()+height()/2
        );
    }
}

main.cpp

#include "mainwindow.h"
#include  <QApplication>

int main(int argc, char *argv[])
{
    QApplication a(argc, argv);
    MainWindow w;

    w.resize(550, 450);
    w.setWindowTitle(QString::fromLocal8Bit("행렬을 이용한 회전"));
    w.show();

    return a.exec();
}

#include <iostream>
#include <vector>
#include <algorithm>
#include <string>

struct Weapon
{
   string name;
   int power;
   int max_use;
   Weapon() {}
   Weapon(string name, int power, int max_use)
      :name(name), power(power), max_use(max_use) {}
   void print() const {
      cout << name << "\t" << power << "\t" << max_use << endl;
   }
};

template  <typename T>
struct SortPower
{
   bool operator()(const T& l, const T& r) const {
      return l.power < r.power;
   }
};

template  <typename T>
struct BinWSearch
{
   bool operator()(const T& w1, const T& w2) const{
      cout << w1.power << ", " << w2.power << endl;
      return w1.power< w2.power;
   }
};

int main()
{

   vector wVec;
   wVec.push_back(Weapon("Sword   ", 45, 50));
   wVec.push_back(Weapon("X-Caliber", 64, 80));
   wVec.push_back(Weapon("Bow     ", 72, 20));
   wVec.push_back(Weapon("Revolver", 87, 20));
   wVec.push_back(Weapon("Shotgun ", 92, 10));

   sort(wVec.begin(), wVec.end(), SortPower());
   for (auto iter = wVec.begin(); iter != wVec.end(); iter++) {  //정렬상태 확인
      iter->print();
   }

   bool found = binary_search(wVec.begin(), wVec.end(), 
   Weapon("X-Caliber", 64, 80), BinWSearch());

   cout << (found ? "검색성공" : "검색실패") << endl;

   cout << "프로그램 종료" << endl;
   return 0;
}

사원수의 기본적인 형태

q = [ w, xi, yj, zk ]

 - w : scalar

 - xi, yj, zk : 허수로 표현된 벡터

스칼라를 제외한 허수들은 벡터를 난타낸다. 그러므로 아래처럼 간략하게 나타내기도 한다

q = [ w, v ]

단위 사원수

q = [ 1, 0, 0, 0 ]

단위 사원수의 경우, 절대값(크기)이 1이다.

|| q || = sqrt(w^2 + x^2 + y^2 + z^2) = 1,  w^2 + x^2 + y^2 + z^2 = 1

사원수 크기 ( Length, Norm)

|| q || = Norm(q) = sqrt(w^2 + x^2 + y^2 + z^2)

정규화(단위사원수 생성) : 사원수의 크기로 사원수를 나눈다

q = q / || q || = q / sqrt(w^2 + x^2 + y^2 + z^2)

켤레 사원수

[ w, xi, yj, zk ]의 켤레 사원수는 [ w, -xi, -yj, -zk ]

사원수의 역수

사원수 q의 역수 = (켤레 사원수) / || q ||^2, 그러므로 크기가 1인 경우, 역수=켤레사원수

단위 사원수의 역수 = 켤레 사원수 (단위사원수는 크기가 1이므로 )

회전을 위한 사원수(회전축, 회전량을 표현함)

q = [ cos(θ/2), xsin(θ/2), ysin(θ/2), zsin(θ/2) ] = [ cos(θ/2), v*(θ/2) ]

 - x, y, z : 회원축을 나타내는 단위벡터(v)

 - θ : 회전량(Radian)

 - 이렇게 설정했을 때 단위 사원수가 됨

점(벡터) 회전을 위한 곱셈

q´ = q v q-1, (v = [0, v])

q' : 벡터 v가 회전변환된 결과 벡터를 포함한 사원수

q : 회전을 위한 사원수(회전축과 회전량 포함)

v : 회전 대상 점(벡터)을 사원수 형식으로 표현 ( v = [0, v] ), 일반벡터 앞에 0을 추가한 것

q-1 : 사원수 q의 역수(단위 사원수의 역수는 켤레 사원수와 같다)

사원수의 곱셈규칙

q1=(w1, x1, y1, z1);        q2=(w2, x2, y2, z2);

위의 각 사원수에서 벡터부를 아래처럼 표현할 수 있다

v1 = (x1, y1, z1),             v2 = ( x2, y2, z2 )

q1 * q2 = ( w1*w2 - v1.Dot(v2),   v2*w1 + v1*w2 + v1.Cross(v2 ) )

위의 식을 가감승제로만 표현하면 다음과 같다

w = w1w2 - x1x2 - y1y2 - z1z2

x = w1x2 + x1w2 + y1z2 - z1y2

y = w1y2 + y1w2 + z1x2 - x1z2

z = w1z2 + z1w2 + x1y2 - y1x2

참고 : 벡터의 외적(Cross Products)

사원수 나눗셈 규칙

https://kr.mathworks.com/help/aeroblks/quaterniondivision.html

The Quaternion Division block divides a given quaternion by another.

The quaternions have the form of

q=q0+iq1+jq2+kq3

and

r=r0+ir1+jr2+kr3.

The resulting quaternion from the division has the form of

t=qr=t0+it1+jt2+kt3,

사원수를 이용하여 공간상의 특정 점(벡터)을 회전하는 예

#include <iostream>
#include <cmath>

using namespace std;

struct Vector
{
	float x, y, z;
	Vector() {}
	Vector(float x, float y, float z) :x(x), y(y), z(z) {}
	/* Dot Product
		v = [x, y, z]
		v'= [x',y',z']
		Dot(v) = xx' + yy' + zz'
	*/
	float Dot(const Vector& v2) const {
		return x * v2.x + y * v2.y + z * v2.z;
	}
	/* Cross Product
		v = [x, y, z]
		v'= [x',y',z']
		v x v' = [yz'-zy', zx'-xz', xy'-yx']
	*/
	Vector Cross(const Vector& v2) const {
		return Vector(
			y*v2.z - z * v2.y,
			z*v2.x - x * v2.z,
			x*v2.y - y * v2.x);
	}
	Vector operator*(float scalar) const {
		return Vector(x*scalar, y*scalar, z*scalar);
	}
	Vector operator+(const Vector& v2) const {
		return Vector(x + v2.x, y + v2.y, z + v2.z);
	}
	float length() {
		return sqrt(x*x + y * y + z * z);
	}
};

struct Quaternion
{
	float w;
	Vector v;
	Quaternion() {}
	Quaternion(float w, float x, float y, float z)
		:w(w), v(Vector(x, y, z)) {}
	Quaternion(const Vector& n, float a)
	{
		a = 3.14159F / 180.0F * a;
		w = cos(a / 2);
		v.x = n.x*sin(a / 2);
		v.y = n.y*sin(a / 2);
		v.z = n.z*sin(a / 2);
	}
	Quaternion(float w, Vector v) : w(w), v(v) {}
	/*
	q1 * q2 = (w1,v1) * (w2,v2) =
	( w1w2-v1.Dot(v2), w1v2 + w2v1 + v1.Cross(v2) )
	*/
	Quaternion operator*(const Quaternion& q) const {
		Quaternion r;
		r.w = w * q.w - v.Dot(q.v);
		r.v = q.v*w + v * q.w + v.Cross(q.v);
		return r;
	}
	const Vector rotate(const Vector& V) const {
		Quaternion p;
		p.w = 0;
		p.v = V;

		const Quaternion& q = (*this);
		return (q * p * q.Invert()).v;
	}
	Quaternion Invert() const {
		//단위 쿼터니언의 역수는 켤레 사원수와 같으므로
		return Quaternion(w, Vector(-v.x, -v.y, -v.z));
	}
	float magnitude() {
		return sqrt(w*w + v.x*v.x + v.y*v.y + v.z*v.z);
	}
};

int main()
{
	//Quaternion(사원수)
	Quaternion q1(Vector(1, 0, 0), 90);
	Quaternion q2(Vector(0, 1, 0), 90);
	Quaternion q3 = q1 * q2;

	cout << "w:" << q2.w << ", x:" << q2.v.x << ", y" << q2.v.y << ", z:" << q2.v.z << endl;
	cout << "크기:" << q2.magnitude() << endl;

	Vector v1(0, 0, 1);
	Vector v2 = q1.rotate(v1); //x축 중심 90도 회전
	cout << "v2, x:" << v2.x << ", y:" << v2.y << ", z:" << v2.z << endl; // y:-1
	cout << "v2 결과벡터 크기:" << v2.length() << endl; // 1

	Vector v3 = q2.rotate(v1); //y축 중심 90도 회전
	cout << "v3, x:" << v3.x << ", y:" << v3.y << ", z:" << v3.z << endl; // x:1
	cout << "v3 결과벡터 크기:" << v3.length() << endl; // 1

	/*
	Quaternion q(Vector(1, 0, 0), 90);
	cout << "크기:" << q.magnitude() << endl; //1
	*/

	return 0;
}

위의 코드를 실행하면 다음과 같은 결과를 볼 수 있다